The Iteration Limits
For the images on this site the unbound criterion for the iteration is |Zn|2>=10. This means the iteration stops if the point Zn lies not inside of a circle with radius sqrt(10) (arround the origin). The starting point of this iteration will then be supposed not to belong to the mandelbrot set.
The number n of iterations of course, which would be necessary to check this unbound criterion could potentially be infinite. For practical reasons it must be stopped after a finite number of steps. Therefore a maximum iteration depth has to be used. If the starting point is not excluded from the set until n has reached this maximum iteration depth, it will be assumed to belong to the mandelbrot set. For dedicated pictures on this site we used a maximum of more than 400e6.
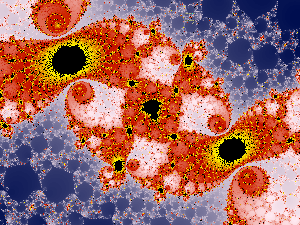
The higher this value is chosen the more accurate is the resolution of the boundary of mandelbrot set - it will be 'sharper'. If it is not high enough the boundary of the black mandel set area will be frayed, parts of the edge are black, or in the worst case, the whole image is black, although it should still show structure of the edge of the mandlbrot set. The black circular parts in the upper and lower areas of the image on the right, for example, should show structure, they do not belong to the mandelbrot set. And the central element should show the mandel bulbs (the apple man) but is nearly degenerated to a frayed circle. Click onto the image to compare it with an image with an approprate iteration depths.
The Coloring
The coordinates of a two dimensional image can naturally be mapped to such complex numbers used in the formula, depending on the image size and the selected range for the x and y coordinate. The pictures are generated by computing the iterations for each point within a chosen rectangular area and resolution. The points which are not belonging to the mandelbrot set, are colored according to the number of iterations (the iteration depth or iteration value of this point/pixel) at which the exclusion was discovered. The mandelbrot set itself is shown as a black area while areas of other colors are showing the edge of the set. In some cases the color black was also used at the edge for a better optical effect.