The Colormap
In earlier times there were technical restrictions that enforced the usage of a colormap with a very limited size (i.e. 256). Nowadays it is possible to directly show any color you want inside a window. So, why still use a colormap for coloring a raster area, when it is possible to directly assign colors to iteration values?
There are good reasons for this. The short answer is: it significantly simplifies the work of coloring an image. The longer answer follows now.
The Coloring Problem
When looking at the iteration depth for every pixel of an images required to detect whether the point belongs to the mandelbrot set or not, you will see that the depths gets the higher the nearer you approach to the edge of the mandelbrot set. This border has a fractal character, meaning that endlessly new structures appear when magnifying this edge.
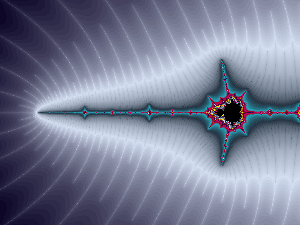
In contrast the resolution of the image is always limited. So when choosing the coordinates of a point in the complex plane assigned to an image pixel near the edge of the set, you get arbitrarily high iteration depths. More important is that they look like randomly scattered in an increasing range of iteration values the nearer you get to the edge. To see what is meant, just have a look at the image below near the edge of the black mandelbrot set area.
The task now is to choose a smooth color gradient for the increasing iteration values from the outermost (lowest number) areas of the image to the innermost areas (highest numbers) near the edge of the mandelbrot set.
So, what happened if you are going to choose colors per existing iteration value for a raster image? If you start from the root area it is sufficient to choose very low limits for the iteration number to achieve a sharp edge of the set and it is quite easy to choose approprate colors for the iteration values found.
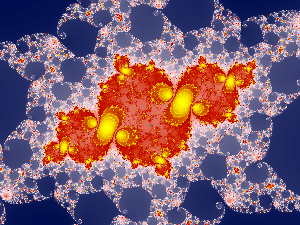
But when diving deeper the required iteration limit is getting higher and higher and you will figure out that there is no equal distribution of iteration values. Additionally the image areas covered with single iteration values at the upper end of the value spectrum gets smaller and smaller. Therefore you need a very flat color gradient here to a achieve an appealing result. Otherwise you only get pseudo-randomly distributed colors for areas near the edge. This is shown in the image to the left. As a result the color mapping at the upper end of the spectrum looks quite boring, there are many iteration values, but the colors should not differ significantly. So, defacto you still have much less different colors to choose, than there are different iteration values in the image raster. It is not a fun to create such color mappings.
If you dive even deeper into the border of the set you may reach iteration depths of several millions. Here this effect gets even more drastically. Because of the limited resolution of the image only few of the iteration values in the range between the outermost and innermost ones really appear in the raster. There cannot exist more real values than the number of pixels of the image, regardless of the range of iteration values covered by the image area.
If you select the right spots another phenomenom gets disturbing the coloring process. It happens that far away from the edge there are narrow passages between parts of the mandelbrot set. Before and after such passages the areas covered with the same iteration values are significantly large enough to require special attention when coloring the image. But inside the passage the iteration values are increasing dramatically and each value covers only a very small portion of the image, if at all. The grade is the steeper the closer the passage is. So the problem already described above not only appears at the upper end of the iteration value spectrum, but might happen anywhere in between, also.
The Solution
The solution for the coloring problem is to use a colormap with a limited, but not necessarily fixed size. Typically a size between several 100 and few thousand entries is sufficient. The maximum size used for the images on this site is below 2000. Basically in most cases the original size of 256 is sufficient to achieve appealing results.